A binary tree is a hierarchical data structure in which each node has at most two children, commonly referred to as the left child and right child. It is widely used in various applications like searching, sorting, and so on.
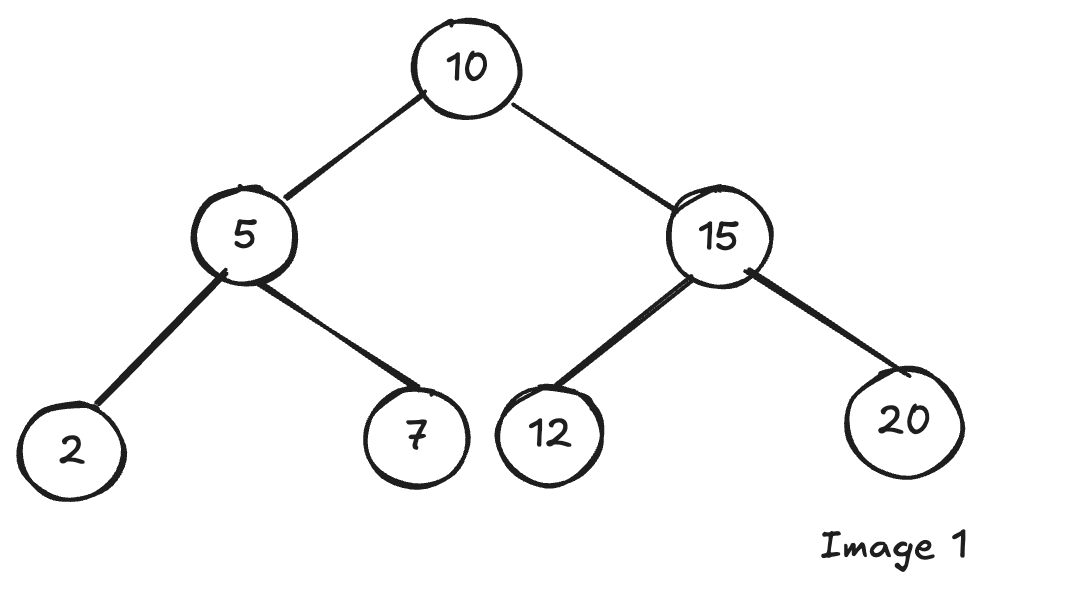
A Binary Search Tree (BST) is a special type of binary tree where each node follows a specific ordering rule: The left subtree contains nodes with values less than the parent node. The right subtree contains nodes with values greater than the parent node (See: Image 1).
Now, let’s jump into the implementation for better understanding. As you can understand from the binary tree structure, each node has two pointers (one for the left and one for the right child node) besides its own value. Let’s start with creating this struct:
type Node struct {
Value int
Left *Node
Right *Node
}
Now, we have the smallest element of our tree, a node. We should be able to add some children to our node to have a BST. Let’s implement the Insert method.
func (n *Node) Insert(value int) {
// As you can recall from our BST definition, we should
// insert the child to the left of the parent if the
// value of the child is smaller than the parent's, and
// vice versa.
if value < n.Value {
// The value is smaller than the parent, we should add
// new value to the left!
if n.Left == nil {
// If the left side is empty, we can simply put our new
// value there.
n.Left = &Node{Value: value}
} else {
// If there is already a node on the left side of our parent node,
// we should re-run the Insert procedure, but now the new parent
// node is the left child of our current parent node. If you got
// confused by the recursion, just go back to Image 1 and imagine
// that we are going to add "1" to our tree while we follow BST
// rules. You will get it easily.
n.Left.Insert(value)
}
} else if value > n.Value {
// We follow the same procedure but go with the right side
// if the new value is greater than the current value
if n.Right == nil {
n.Right = &Node{Value: value}
} else {
n.Right.Insert(value)
}
}
}
That was the insertion procedure. Let’s continue with the search operation. I’m going to name the method as “Has”, because we are basically looking for whether our tree has a specific value or not.
func (n *Node) Has(value int) bool {
// We will just recursively check the right and left
// children of a node, and if we find a node with the
// same value we are searching for, we will return true.
if n == nil {
// If, somehow, we encounter a nil node, that means we
// don't have the value that we are looking for.
return false
}
if n.Value == value {
// We found it!
return true
}
// Search the left subtree
if n.Left.Has(value) {
return true
}
// Value was not in the left subtree, let's look to the
// right subtree.
if n.Right.Has(value) {
return true
}
// The code reached here means we don't have the
// value in this tree.
return false
}
Now, let’s look at how we can remove a value from the tree. Deletion in a BST is a bit more involved than insertion or search because we need to maintain the BST properties after removing a node.
There are three main scenarios we need to handle:
- The node has no children: This is the simplest case — we just return nil to remove the node.
- The node has one child: We return that child to replace the node we’re deleting.
- The node has two children: This is the trickiest case. We find the smallest value in the right subtree (called the in-order successor), assign it to the current node, and then recursively remove that successor node from the right subtree.
Let’s explain each scenario with the implementation:
func (n *Node) Remove(value int) *Node {
if n == nil {
return nil
}
if value < n.Value {
n.Left = n.Left.Remove(value)
} else if value > n.Value {
n.Right = n.Right.Remove(value)
} else {
// We found the node to be deleted
if n.Left == nil && n.Right == nil {
return nil
}
if n.Left == nil {
return n.Right
}
if n.Right == nil {
return n.Left
}
successor := n.Right.Min()
n.Value = successor
n.Right = n.Right.Remove(successor)
}
return n
}
Let’s walk through an example. Suppose we want to remove the value 2 from our BST:
root = root.Remove(2)
We first hit the condition value < n.Value, so we go left. n.Left is the node with value 5. So now we're at node 5, and again value < n.Value, so we go left again and finally reach node 2.
Now we’ve found the node to delete. Since 2 is a leaf node (no children), we return nil. This gets assigned back to the .Left of the previous node (5), effectively removing 2 from the tree:
n.Left = n.Left.Remove(2) // becomes n.Left = nil
That’s how we remove leaf nodes in a BST.
But what if the node has one child?
For example, if node 2 had a left child 1, we wouldn’t return nil. Instead, we would return the child itself:
if n.Left == nil {
return n.Right
}
if n.Right == nil {
return n.Left
}
So in this case, node 2 gets replaced by node 1, and the BST structure remains valid.
Now for the most complex case — removing a node with two children.
Let’s say we want to remove the value 5 from the tree. Since it has both Left and Right children, we can’t just delete it. Instead, we replace it with a value that keeps the tree ordered correctly.
The most common approach is to replace it with the smallest value in the right subtree — also known as the in-order successor:
successor := n.Right.Min()
n.Value = successor
n.Right = n.Right.Remove(successor)
Why do we pick the smallest value in the right subtree?
Because it’s the next greater value in the tree — it’s guaranteed to be larger than all values in the left subtree and smaller than everything else in the right subtree. That makes it a perfect replacement that maintains the BST ordering.
(You could also choose the largest value in the left subtree — the in-order predecessor — and follow the same approach.)
Here’s the Min() method we use to find the in-order successor:
func (n *Node) Min() int {
// We simply return the leftmost value
for n.Left != nil {
n = n.Left
}
return n.Value
}
One of the most confusing processes in BSTs is the level-order traversal. In this traverse method we have to visit each node of the tree level by level and process them in order.
Imagine our example tree (Image 1). We should visit 10-5-15–2-7-12-20 in order. Imagine we start with the root (10), we printed it, and we went to left side (5), we printed it too, then how can we go to right of the node 10 and print 15?
Nodes don’t store references to their parents or siblings. This is why we use queues in level order traversal. We will enqueue the parent node, process it, dequeue it and add its children to the queue if they existed. We will repeat this in a loop until the queue is empty.
Let’s see the implementation:
func (n *Node) LevelOrder() {
if n == nil {
return // Nothing to process if the tree is empty
}
// We use a slice as a queue and start with the root node
queue := []*Node{n}
for len(queue) > 0 {
// Take the first node out of the queue
current := queue[0]
queue = queue[1:]
// Print the current node's value
fmt.Print(current.Value, " ")
// Add left child to the queue if it exists
if current.Left != nil {
queue = append(queue, current.Left)
}
// Add right child to the queue if it exists
if current.Right != nil {
queue = append(queue, current.Right)
}
}
}
Final Thoughts
Binary Search Trees are useful data structures that combine the binary trees with ordered data storage, making operations like search, insert, and delete efficient — especially when the tree is balanced. In this post, I tried to explain the basic functionalities of the BSTs with the implementation details for better understanding. The real applications usually use self-balancing versions like AVL or Red-Black Trees to keep performance consistent but in this post, I skipped those ones to make the post more beginner-friendly. Learning how a basic BST works is essential before moving on to more complex ones. I hope this post makes BST clearer to you!
“Writing is seeing the future.” Paul Valéry