
Binary tree, her düğümün en fazla iki çocuğa sahip olabileceği hiyerarşik bir veri yapısıdır. Bu çocuk düğümler genellikle left child (sol çocuk) ve right child (sağ çocuk) olarak adlandırılır. Binary tree yapıları; arama, sıralama gibi pek çok farklı uygulamada yaygın şekilde kullanılır.
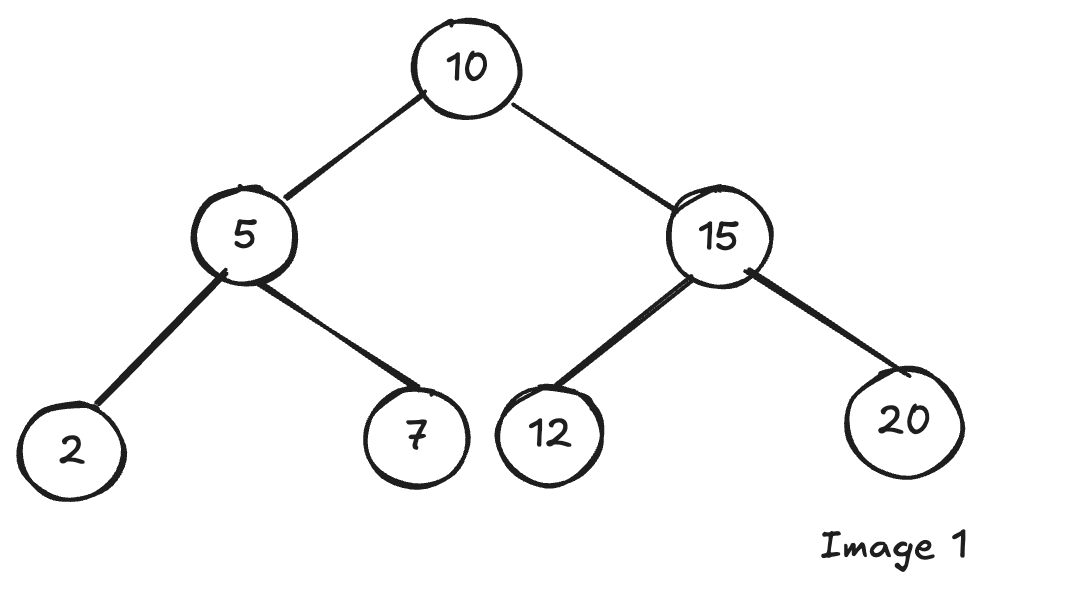
Binary Search Tree (BST) ise, her düğümün belirli bir sıralama kuralına uyduğu özel bir binary tree türüdür: Sol alt ağaç, değeri ebeveyn düğümden küçük olan düğümleri içerirken; sağ alt ağaç, değeri ebeveyn düğümden büyük olan düğümleri içerir. (Bkz: Görsel 1)
Şimdi daha iyi anlayabilmek için implementasyona geçelim. Binary tree yapısından da anlayabileceğiniz gibi, her düğüm kendi değerinin yanı sıra iki adet pointer barındırır: biri sol çocuğu, diğeri ise sağ çocuğu işaret eder. Bu yapıyı temsil eden struct’ı oluşturarak başlayalım:
type Node struct {
Value int
Left *Node
Right *Node
}
Artık elimizde ağacımızın en küçük yapı taşı olan bir node var. Bu düğüme çocuk düğümler ekleyerek bir BST yapısı oluşturabilmeliyiz. Bunu gerçekleştirebilmek için, Insert metodunu implement edelim.
func (n *Node) Insert(value int) {
// BST tanımımızdan hatırlayacağınız üzere,
// eğer eklenecek değerin parent (ebeveyn) düğümün değerinden küçükse
// bu düğümü parent’ın soluna eklemeliyiz;
// aksi durumda ise sağına eklemeliyiz.
if value < n.Value {
// Değer, parent düğümden küçük — yeni değeri sol tarafa eklemeliyiz!
if n.Left == nil {
// Eğer sol taraf boşsa, yeni değeri doğrudan oraya yerleştirebiliriz.
n.Left = &Node{Value: value}
} else {
// Eğer parent düğümümüzün sol tarafında zaten bir node varsa,
// Insert işlemini tekrar çalıştırmamız gerekir — ancak bu kez
// yeni parent node, mevcut parent’ın sol çocuğu olacaktır.
// Eğer bu rekürsif yapı kafanızı karıştırdıysa Görsel 1’e geri dönün
// ve BST kurallarını takip ederek ağaca “1” değerini eklemeye
// çalıştığınızı hayal edin. Ne demek istediğimizi kolayca anlayacaksınız.
n.Left.Insert(value)
}
} else if value > n.Value {
// Aynı işlemi bu kez sağ taraf için uyguluyoruz,
// çünkü yeni değer mevcut düğümün değerinden büyük.
if n.Right == nil {
n.Right = &Node{Value: value}
} else {
n.Right.Insert(value)
}
}
}
Ekleme işlemi bu şekildeydi. Şimdi arama (search) işlemiyle devam edelim. Bu yönteme “Has” adını vereceğim çünkü temel olarak ağacımızda belirli bir değerin olup olmadığını kontrol edeceğiz.
func (n *Node) Has(value int) bool {
// Sağ ve sol çocuk düğümleri rekürsif olarak kontrol edeceğiz.
// Eğer aradığımız değere sahip bir düğüm bulursak, true döneceğiz.
if n == nil {
// Eğer herhangi bir şekilde nil bir düğümle karşılaşırsak,
// bu aradığımız değerin ağacımızda olmadığını gösterir.
return false
}
if n.Value == value {
// Değeri bulduk!
return true
}
// Sol alt ağacı arıyoruz
if n.Left.Has(value) {
return true
}
// Değer sol alt ağaçta bulunamadı, şimdi sağ alt ağaca bakalım.
if n.Right.Has(value) {
return true
}
// Kodun buraya ulaşması değerin ağaçta bulunmadığını gösterir.
return false
}
Şimdi ise ağacımızdan bir değeri nasıl silebileceğimize bakalım. BST’de silme işlemi, ekleme veya arama işlemlerine göre biraz daha karmaşıktır çünkü bir düğümü sildikten sonra BST’nin sıralama kurallarını korumamız gerekir.
Bu işlemde karşılaşacağımız üç temel durum vardır:
- Düğümün çocuğu yoksa: En basit durumdur — düğümü kaldırmak için nil döneriz.
- Düğümün bir çocuğu varsa: Silinen düğüm yerine o çocuğu koyarız.
- Düğümün iki çocuğu varsa: En karmaşık durumdur. Sağ alt ağaçta bulunan en küçük değeri (in-order successor) buluruz, bu değeri mevcut düğüme atarız ve ardından bu successor düğümü sağ alt ağaçtan sileriz.
Şimdi her durumu kod ile açıklayalım:
func (n *Node) Remove(value int) *Node {
if n == nil {
return nil
}
if value < n.Value {
n.Left = n.Left.Remove(value)
} else if value > n.Value {
n.Right = n.Right.Remove(value)
} else {
// Silinecek düğümü bulduk
if n.Left == nil && n.Right == nil {
return nil
}
if n.Left == nil {
return n.Right
}
if n.Right == nil {
return n.Left
}
successor := n.Right.Min()
n.Value = successor
n.Right = n.Right.Remove(successor)
}
return n
}
Bir örnekle ilerleyelim. Diyelim ki BST’mizden 2 değerini silmek istiyoruz:
root.Remove(2)
Öncelikle value < n.Value koşulunu sağladığımız için sola geçiyoruz. n.Left düğümü değeri 5 olan düğüm. Şimdi 5 düğümündeyiz ve yine value < n.Value olduğu için tekrar sola iniyoruz ve sonunda 2 düğümüne ulaşıyoruz.
Silinecek düğümü bulduk. 2, yaprak düğüm (çocuğu yok) olduğu için nil döndürüyoruz. Bu değer, önceki düğümün (5’in) .Left alanına atanıyor ve böylece 2 düğümü ağaçtan efektif olarak silinmiş oluyor:
n.Left = n.Left.Remove(2) // artık n.Left = nil oldu
BST’de yaprak düğümler bu şekilde silinmektedir.
Peki ya silinecek düğümün bir çocuğu varsa?
Örneğin, 2 düğümünün solunda 1 değerini taşıyan bir çocuk node varsa, bu durumda nil döndürmeyiz. Bunun yerine, o çocuğun kendisini döneriz:
if n.Left == nil {
return n.Right
}
if n.Right == nil {
return n.Left
}
Bu durumda, 1 düğümü 2 düğümünün yerini alır ve BST yapısı geçerliliğini korur.
Şimdi en karmaşık duruma gelelim — iki çocuğu olan bir düğümün silinmesi.
Diyelim ki ağaçtan 5 değerini silmek istiyoruz. Hem sol hem sağ çocuğu olduğu için doğrudan silemeyiz. Bunun yerine, ağacın sıralamasını koruyacak bir değerle değiştirmemiz gerekir.
En yaygın yöntem, sağ alt ağaçtaki en küçük değerle — yani in-order successor ile — değiştirmektir:
successor := n.Right.Min()
n.Value = successor
n.Right = n.Right.Remove(successor)
Neden sağ alt ağaçtaki en küçük değeri seçiyoruz?
Çünkü o, ağacın bir sonraki en büyük değeridir — sol alt ağaçtaki tüm değerlerden büyük, sağ alt ağaçtaki diğer tüm değerlerden ise küçüktür. Bu nedenle, BST sıralamasını koruyan mükemmel bir yer değiştirme değeri olur.
(Aynı mantıkla, sol alt ağaçtaki en büyük değer — yani in-order predecessor — da seçilebilir ve benzer şekilde işlem yapılabilir.)
İşte in-order successor’ı bulmak için kullandığımız Min() metodu:
func (n *Node) Min() int {
// En sola doğru ilerleyerek en küçük değeri döndürüyoruz
for n.Left != nil {
n = n.Left
}
return n.Value
}
BST’lerde en karışık konulardan biri seviye sırasına göre dolaşma (level-order traversal) yöntemidir. Bu yöntemle, ağacın düğümlerini seviye seviye ziyaret edip, sırayla işlememiz gerekir.
Örnek ağacımızı (Görsel 1) düşünelim. Ziyaret sıramız şöyle olmalı: 10-5-15-2-7-12-20. Kök düğümle (10) başlayıp onu yazdırdık, sonra sol çocuğa (5) geçtik ve onu da yazdırdık. Peki, 10 düğümünün sağındaki 15 düğümüne nasıl geçip onu yazdıracağız?
Düğümler, ebeveynlerine veya kardeşlerine referans tutmazlar. İşte bu yüzden seviye sırasına göre dolaşmada queue (kuyruk) kullanırız. Önce parent düğümü kuyruğa ekler, onu işler, kuyruktan çıkarır ve varsa çocuklarını kuyruğa ekleriz. Bu işlemi kuyruk boşalana kadar döngü ile tekrarlarız.
Şimdi implementasyona bakalım:
func (n *Node) LevelOrder() {
if n == nil {
return // Ağaç boşsa işlenecek bir şey yok
}
// Queue olarak bir slice kullanıyoruz ve kök düğümle başlıyoruz
queue := []*Node{n}
for len(queue) > 0 {
// Queuedan ilk düğümü çıkarıyoruz
current := queue[0]
queue = queue[1:]
// Mevcut düğümün değerini yazdırıyoruz
fmt.Print(current.Value, " ")
// Sol çocuk varsa queueya ekliyoruz
if current.Left != nil {
queue = append(queue, current.Left)
}
// Sağ çocuk varsa queueya ekliyoruz
if current.Right != nil {
queue = append(queue, current.Right)
}
}
}
Sonuç
Binary Search Tree (BST), binary ağaç yapısını sıralı veri saklama ile birleştiren ve arama, ekleme, silme gibi işlemleri özellikle dengeli olduğunda oldukça verimli hale getiren faydalı bir veri yapısıdır. Bu yazıda, BST’nin temel fonksiyonlarını ve anlaşılmasını kolaylaştırmak için implementasyon detaylarını anlatmaya çalıştım. Gerçek uygulamalarda performansın tutarlı olması için genellikle AVL veya Red-Black Tree gibi kendi kendini dengeleyen versiyonları kullanılır; ancak bu yazıda başlangıç seviyesine uygun olması adına bu yapıları dahil etmedim. Temel bir BST’nin nasıl çalıştığını öğrenmek, daha karmaşık ağaç yapılarına geçmeden önce faydalı olabilir. Umarım bu yazı, BST’leri daha iyi anlamanıza yardımcı olmuştur!
“Yazmak, geleceği görmektir.” Paul Valéry

